A gentle introduction to the standard error of the mean
Imagine if you were working for a company that wanted to know the mean number of page views their website received per day. How do you measure this? Well, the most logical thing to do is to pick a sample of days, record the number of page views, and take the mean of these. However, how do you know if this is the true mean number of page views per day? How do you know if you’ve taken a big enough sample?
The first thing to understand is that we are talking about two different means. The first is the true mean (or population mean) number of page views per day, which we would get if we took every day that the site has been in existence and took the mean of the daily page views. The other is the sample mean number of page views per day, which we would get if we took a representative sample of days and took the mean of their daily page views. (I will talk more about selecting a representative sample in a later blog post - stay tuned!)
The standard error of the mean (or SEM) is the amount our sample mean might differ from the true mean. In our page views example, this means we are trying to find out how much possible “fuzziness” there is in our sample mean number of daily page views as an estimate of the true mean. Is it likely our estimate might be out by a couple of page views per day? Or could it be as much as 100? Obviously, the smaller the standard error of the mean, the better the sample estimate reflects the true population value. There are formulas for calculating the SEM depending on the distribution you are dealing with, but the main focus of this blog post will be describing the general principles underlying it.
Why should I care about the standard error of the mean?
It is easy once you get into applying statistics to a sample to forget you are dealing with a representation of a population, rather than the population itself. As such, all statistics you derive using your sample are just estimates of the true population parameters you are hoping to talk about. It is therefore important that you have some idea how reliable these estimates are before you start inferring from them.
How is the standard error of the mean calculated?
One way of assessing the SEM is to sample repeatedly from the population, calculate the mean for each sample, and plot the distribution of these means. Each sample is expected to be a different representation of the population, with different estimates of the mean in each sample.
Let’s revisit our problem of assessing the accuracy of the mean number of page views. One thing you could do is take a large number of samples of 30 day periods each, where large means 1,000 or more. Instead of doing this (because it would take about 82 years…), let’s pretend we already know the population mean and distribution and simulate this result in R. In this case, let’s say we have an mean of 220 page views per day, which we would model using a Poisson distribution (i.e., \(\lambda\) = 220/day). (As you may already know, we use the Poisson distribution as it is the most appropriate distribution for describing a count of events occurring over time.)
# Clear the workspace
rm(list = ls())
# Set seed to replicate random variable generation
set.seed(567)
# Generate the mean of each sample and store in a vector, and store each sample in a dataframe
mn_vector <- NULL
sample_frame <- data.frame(row.names = seq(from = 1, to = 30, by = 1))
for (i in 1 : 1000) {
s <- rpois(30, lambda = 220)
sample_frame <- cbind(sample_frame, s)
mn_vector <- c(mn_vector, mean(s))
}
# Name the columns in the sample dataframe
names(sample_frame) <- paste0("n", seq(from = 1, to = 1000, by = 1))
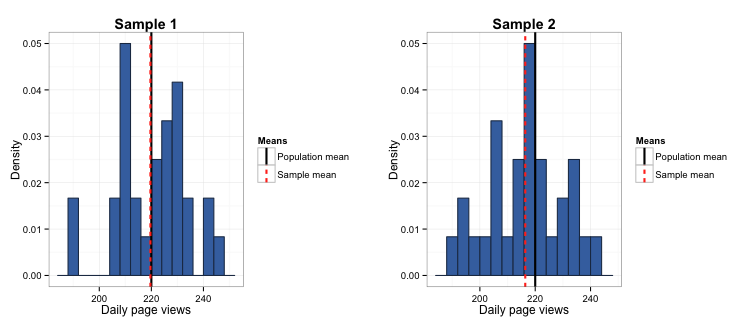
When we do this, our first sample has a mean rate of 220 page views per day, and our second sample has a mean rate of 216 page views per day. Looking at the sample distributions (below), the sample mean almost completely mirrors the population mean in sample 1, but there is quite a bit of difference between the two values in sample 2.
Now we plot the distribution of the means of each of the 1,000 samples. Remember we are no longer looking at how much each daily page view varies from each other; instead, we are looking at how much each of the means of these samples of 30 days of page views differ from each other (it’s like, a total meta-distribution).
It turns out that the distribution of the mean of the samples is approximately normally distributed (as described by the Central Limit Theorem). This does depend on your observations (i.e., each day of page views) being independent and identically distributed (or iid), which basically means each observation has been sampled from the same distribution, and the value of any observation in the sample is not dependent on the values of other values in the sample. In our case, the page views would be iid if each was from a Poisson distribution with \(\lambda\) = 220, and the page views you receive on one day are not influenced by the page views on another day.
This can be seen in the histogram of the means of each sample:
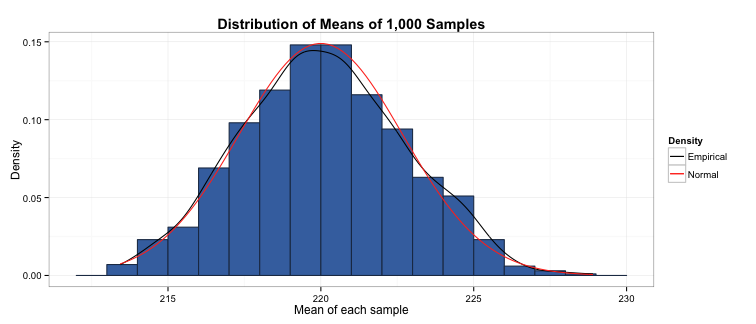
The mean of this distribution should be a pretty close estimate of the population mean - and it is, equalling 220.1. If we take the standard deviation of this distribution, we get the standard error of the mean. Because these means are normally distributed, ±1 standard error around the mean of the sample means represents the range that 68% of the sample means fall within, ±2 standard errors represents the range that 95% of the sample means fall within, and so on.
In our case, taking a sample of 30 days gives us a pretty accurate assessment of the population mean, with 68% of our samples giving a mean between 217.4 and 222.8, and 95% of our samples giving a mean between 214.8 and 225.3. In other words, 68% of the time when we take a sample we will end up with a mean between 217.4 and 222.8, and 95% of the time when we take a sample we will end up with a mean between 214.8 and 225.3. This is a pretty tight band around our population mean of 220 page views per day, indicating that a sample of 30 gives a pretty good estimate of the mean.

Back to the formula…
As I mentioned at the beginning of this post, the SEM is calculated using a distribution-specific formula. In the case of the Poisson distribution, this is \(\sqrt{\lambda / n}\). Let’s see how this compares to our simulation-based estimation of the SEM.
# Defining lambda and n
lambda <- 220
n <- 30
# Calculating SEM
sem <- sqrt(lambda / n)
Using the formula, the range of mean daily page views falling within ±1 SEM is 217.3 to 222.7, and the range falling within ±2 SEMs is 214.7 to 225.3. This is extremely close to the estimate given using the simulation exercise above.
The take away message
As you can see, the SEM is a useful indication of how likely it is that your sample mean is an accurate reflection of the population value. You can also see it is highly dependent on the size of the sample you choose, with larger samples leading to tighter standard errors. While I have demonstrated calculating the SEM for the mean of a Poisson-distributed variable, the same principles apply with any type of distribution.
Much of the points and code in this blog post are adapted from the excellent Statistical Inference unit on Coursera by Brian Caffo, Jeff Leek and Roger Peng. This course gives a far more comprehensive coverage of this material and is highly recommended.
Finally, the full code used to create the figures in this post is located in this gist on my Github page.
