Representative sampling
Unless we are lucky enough to have access to an entire population and the capacity to analyse all of that data, we have to make do with samples from our population to make statistical inferences. Choosing a sample that is a good representation of your population is the heart of a quality analysis, as all of the fancy statistical tricks in the world can’t make accurate conclusions from bad or biased data. In this blog post, I will discuss some key concepts in selecting a representative sample.
First things first: What is your population of interest?
Obviously it is a bit tricky to get a representative sample if you’re not sure what population you’re trying to represent, so the first step is to carefully consider this question. In the two previous blog posts (here and here), I used the example that your company wanted you to assess the mean daily number of page views their website receives. Well, what mean daily page views do they want to know about?
Let’s consider some complications to that question. The first is seasonality. Your website might receive more hits at certain times of year. Do we want to include or exclude these periods from our population? Another consideration is the demographic profile of the people visiting your website. Are we interested in all visitors? Or do we want visitors of a certain sex, age group or region? A final consideration is whether there has been some sort of change in condition that may have increased the visitors to the site. For example, was there an advertising campaign launched recently? Has the website added additional languages which mean a broader audience can access it? Does the website sell a product that now ships to additional places?
Let’s imagine our website is a retail platform that sells children’s toys. We see some seasonal spikes in page views every year at Easter, Christmas and two major sale periods every year (Black Friday and post-Christmas). No major advertising campaigns are planned outside these seasonal periods, nor any changes planned to the site. Our company want to know what the “typical” number of mean daily page views is outside these seasonal periods. They don’t care about individual demographic groups of visitors, they just want the visitors as a whole. Therefore, we need to find a sample that reflects this.
Choosing a representative sample
Sample size
Sample size is a key element to representative sampling as it increases your chances of gaining sufficient information about the population, rather than having your statistics influenced by anomalous observations. For example, imagine if by chance we sampled a much higher than average value. Let’s see how this influences a sample of 30 page views compared to a sample of 10. We’ll generate samples drawn from a Poisson distribution with a mean of 220 views per day, and add an outlier of 260 views per day to each:
set.seed(567)
# Sample of 30 (29 from the Poisson distribution and an outlier of 260)
sample1 <- c(rpois(29, lambda = 220), 260)
# Sample of 10 (9 from the Poisson distribution and an outlier of 260)
sample2 <- c(rpois(9, lambda = 220), 260)
Compared to the population mean, the mean of the sample of 30 is 221.5 whereas the mean of the sample of 10 is 224.4. As you can see, the smaller sample is far more influenced by the extreme value than the larger one.
A sufficient sample size depends on a lot of things. For example, if the event we were trying to describe was rare (e.g., 1 event per 100 days), a sample of 30 would likely be too small to assess its mean occurrence. When conducting hypothesis testing, the correct sample size is generally calculated using power calculations, something I won’t get into here as it can get veeeeery complicated.
An additional consideration is that overestimating the required sample size can also be undesirable as there may be time, monetary or even ethical reasons to limit the number of observations collected. For example, the company that asked us to assess page views would likely be unhappy if we spent 100 days collecting information on mean daily page views when the same question could be reliably answered from 30 days of data collection.
Representativeness
However, a sufficient sample size won’t be enough if the data are not representative. Representativeness means that the data are sampled from all observations in the population and excludes anything that is outside the population. Representativeness is violated when the sample is biased to a subset of the population or when the sample includes observations from outside the population of interest.
Let’s simulate the number of page views our website received per day in 2014. As you can see in the R code below, I’ve included increased page views for our peak periods of Easter, Black Friday/Christmas, and the post-Christmas sales.
# Simulate some data for 2014, with mean page views of 220 per day.
days <- seq(as.Date("2014/1/1"), as.Date("2014/12/31"), "days")
page.views <- rpois(365, lambda = 220)
views <- data.frame(days, page.views)
# Generate post Christmas sale peak period (January 1-10) with mean page views of 400 per day.
views$page.views[views$days >= "2014/01/01" & views$days <= "2014/01/10"] <- rpois(10, lambda = 400)
# Generate Easter peak period (April 1-21) with mean page views of 350 per day.
views$page.views[views$days >= "2014/04/01" & views$days <= "2014/04/21"] <- rpois(21, lambda = 350)
# Generate Black Friday and Christmas peak periods (November 28-December 31) mean page views of 500 per day.
views$page.views[views$days >= "2014/11/28" & views$days <= "2014/12/31"] <- rpois(34, lambda = 500)
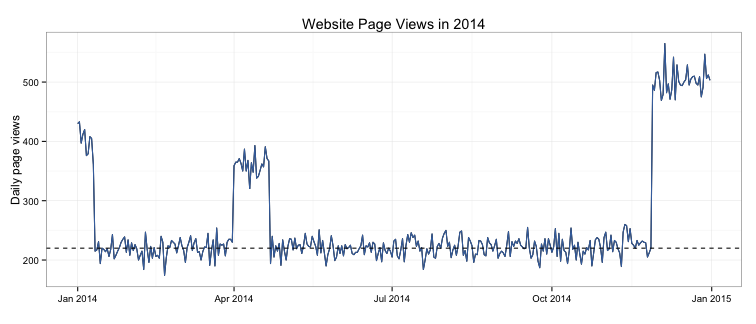
If you look at the graph above, you can see that for most of the year the page views sit fairly consistently around a mean of 220 (as shown in the dotted black line). If we sampled any time outside of the peak periods, we would be pretty safe in assuming we have a representative sample. However, what if we sampled between March 15 and April 14? We would catch some of the Easter peak period in our sample and our sample would no longer represent typical (non-peak) daily page views - instead, we would overestimate our page views by including observations from the peak period population in our sample.
A final thing to consider: the method of measurement
While not part of representative sampling per se, an extremely important and related concept is how the thing you are measuring relates to your concept of interest. Why does our company want to know how many page views we get? Do they specifically want to know how many visitors they receive a day in order to plan things like server demand? Or do they want to extrapolate from number of visitors to comment on something like the popularity of the page? It is important to consider whether the measurement you take is a good reflection of what you are interested in before you make inferences based on your data. This falls under the branch of statistics known as validity, which is again beyond the scope of this post but an extremely interesting topic.
The take away message
I hope this has been a helpful introduction to picking a good sample, and a reminder that even when you have really big data, you can’t escape basic considerations such as what your population is, and whether the variables you have can really answer your question!
Finally, the full code used to create the figures in this post is located in this gist on my Github page.
